「决策树」软决策树的结构与实现

​ 软决策树(SDT)的概念是2017年谷歌大脑团队成员Nicholas Frosst和Geoffrey Hinton在arxiv平台上发布的论文《Distilling a Neural Network Into a Soft Decision》中提出的概念。该决策树主要用来将深度神经网络转换成一个软决策树从而尝试提高决策模型的可解释性。

一、软决策树的定义

​ SDT中每个内部节点i有一个学习滤波器w和一个偏差b，所有叶节点对应一个可学习的概率分布Q。在每个内部节点，采用右子节点的概率为：

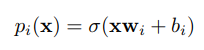
其中x是模型的输入，σ是sigmoid逻辑函数。

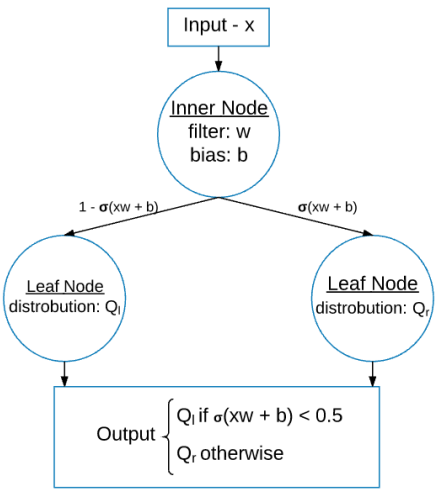
那么深度为1的SDT用于分类任务的计算流程图如下：

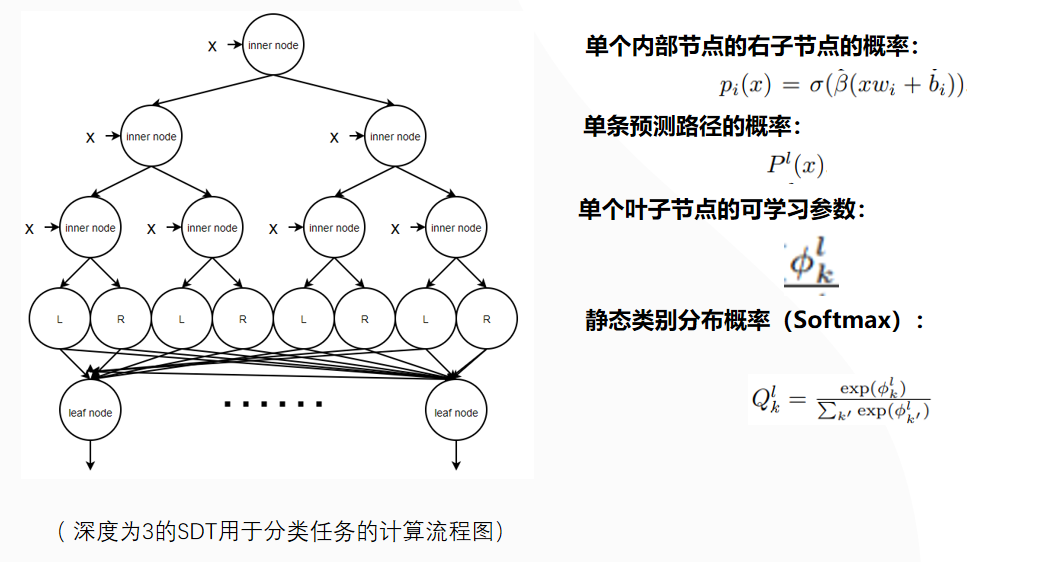
我们列举一个更加复杂的深度为3的SDT用于分类任务的计算流程图：

SDT的损失函数计算如下：

二、软决策树的性能

​ 在SDT的提出论文中提到，SDT开始过拟合的总参数数通常小于多层神经网络开始过拟合的总参数数。在MNIST数据集上进行分类实验时，使用深度为8的软决策树进行训练时测试准确率最多达到94.45%，相比之下具有2个卷积隐藏层和1个全连接层的神经网络的测试精度高达99.21%。

​ 使用由真实标签和神经网络预测组成的软目标进行训练，生成更好的软决策树。用这种方法训练的软决策树达到了96.76%的测试精度，介于神经网络和直接在数据上训练的软决策树之间。

​ 总体上看，软决策树使用学习的过滤器根据输入示例做出分层决策，并最终选择类上的特定静态概率分布作为其输出。这种软决策树比直接对数据进行训练的决策树具有更好的泛化能力，但其性能不如用于为其提供软目标的神经网络。因此，需要解释为什么模型以特定的方式对特定的测试用例进行分类，我们可以使用软决策树。

三、软决策树的实现

1、定义SDT的参数

一个SDT最重要的4个参数是：

input_dim,# 输入数据的维度
output_dim, # 输出数据的维度，（分类任务的类别k）
depth=1, # SDT的深度，必须大于0
lamda=1e-3, # 惩罚项参数，必须大于等于0

首先需要确保SDT的参数输入是正确的：

	# 检查参数是否符合规范
    def _check_validate_parameters(self):
        if not self.depth > 0:
            msg = ("树的深度必须大于0，但是目前设定为：{}")
            raise ValueError(msg.format(self.depth))
        if not self.lamda >= 0:
            msg = ("正则化项的系数不能是负数，但是目前设定位：{} ")
            raise ValueError(msg.format(self.lamda))

然后可以计算得到一个SDT的内置节点和叶子节点的个数：

self.internal_node_num_ = 2 ** self.depth - 1 # SDT中内置节点个数
self.leaf_node_num_ = 2 ** self.depth # SDT中的叶节点个数

例如深度为3时，其内置节点个数为2^3-1=7，叶子节点个数为2^3=8。

2、定义SDT的内置节点

然后就可以定义其对应的self.internal_node_num_个内置节点，这里使用一个全连接层来代替：

self.inner_nodes = t.nn.Sequential(OrderedDict([
            ("Line1", nn.Linear(self.input_dim + 1, self.internal_node_num_, bias=False),),
            ("ReLU", nn.Sigmoid())
        ]))

注意：上述输入维度变成了self.input_dim + 1，这是在输入数据时作者为每个样本添加了一个固定的输入1（论文中没有给出原因）。

# 获取每个内置节点的右分支的输出概率
path_prob = self.inner_nodes(X) # torch.Size([batch_size, internal_node_num_])
# 获取每个内置节点的左右分支的输出概率
path_prob = torch.unsqueeze(path_prob, dim=2) # 升维，torch.Size([batch_size, internal_node_num_，1])
path_prob = torch.cat((path_prob, 1 - path_prob), dim=2) # 拼接，torch.Size([batch_size, internal_node_num_，2])

3、循环计算每条路径概率及其惩罚项

_mu = X.data.new(batch_size, 1, 1).fill_(1.0) # 内置节点的概率乘积，初始设置为1，升维，torch.Size([batch_size, 1，1])
_penalty = torch.tensor(0.0).to(self.device) # 整个树的正则化处罚，0
# 循环获取每层上的内置节点概率
begin_idx = 0 # 第i个层的节点开始序号，包含该序号
end_idx = 1 # 第i个层的节点开始序号，不包含该序号
for layer_idx in range(0, self.depth):
	_path_prob = path_prob[:, begin_idx:end_idx, :] # 获取当前层的所有内置节点概率      	# 计算当前层的正则化处罚
    _penalty = _penalty + self._cal_penalty(layer_idx, _mu, _path_prob) 
    # 调整shape，torch.Size([1, 1, 2])
   	_mu = _mu.view(batch_size, -1, 1) .repeat(1, 1, 2) 
	_mu = _mu * _path_prob  # update path probabilities
    # 更新每层的序号
	begin_idx = end_idx
    end_idx = begin_idx + 2 ** (layer_idx + 1)
    #print("_mu:", _mu.shape) # torch.Size([batch_Size, path_num, 2])
    mu = _mu.view(batch_size, self.leaf_node_num_)