「算法刷题」01背包理论

本博客是记录作者学习最简单的01背包问题的笔记。

一、问题描述

标准的背包问题：有N件物品和一个最多能背重量为W 的背包。第i件物品的重量是weight[i]，得到的价值是value[i] 。每件物品只能用一次，求解将哪些物品装入背包里物品价值总和最大。

二、举例分析

背包：最大重量为4。

物品为：

	重量	价值
物品0	1	15
物品1	3	20
物品2	4	30

问背包能背的物品最大价值是多少？

问题代码定义如下：

vector<int> weight = {1, 3, 4}; //	物品重量
vector<int> value = {15, 20, 30};// 物品价值
int bagWeight = 4;// 背包最大重量

1、定义dp数组的含义

dp(i，j) 表示容量为j的背包从下标为[0-i]的物品里任意取物品的最大价值总和；

// 二维数组
vector<vector<int>> dp(weight.size(), vector<int>(bagWeight + 1, 0));

2、分析推导公式

我们可以按照放物品i和不放物品i两种情况来求出dp(i,j):

dp(i,j)=max(容量为j的背包不放物品i的最大价值，容量为j的背包放物品i的最大价值)。

容量为j的背包，里面不放物品i的最大价值是dp(i-1，j) ;

则容量为j-weight[i]的背包不放物品i的最大价值为dp(i-1,j-weight[i]);

则容量为j的背包里面放物品i的最大价值是dp(i-1,j-weight[i])+value[i]；

所以我们的推导公式为： \(dp(i-1，j) =max(dp(i-1，j),dp(i-1,j-weight[i])+value[i])\)

3、初始化dp数组

容量j为0的背包放任意物品的最大价值都是0，则dp(i,0)=0;

根据推导公式我们也知道，我们也必须知道dp(0,i)的值，即编号0的物品放进容量为j的背包的最大价值

显然当 j < weight[0]时，即编号0的物品重量比背包还重，此时最大价值是0；

当 j >= weight[0]时，即编号0的物品重量比背包请，此时最大价值是value[0]；

// 二维数组
vector<vector<int>> dp(weight.size(), vector<int>(bagWeight + 1, 0)); 
// 初始化
for (int j = weight[0]; j <= bagWeight; j++) {
    dp[0][j] = value[0];
}

初始化结果如图所示：

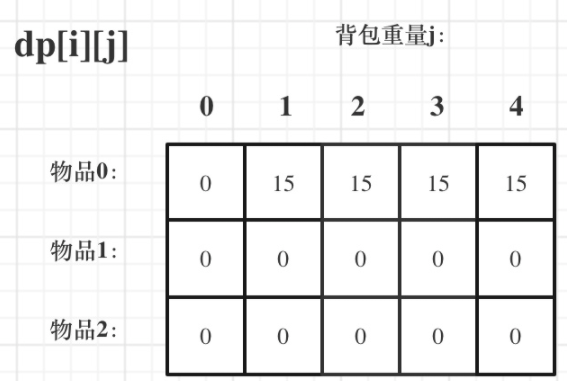
4、推导dp数组

// weight数组的大小 就是物品个数
    for(int i = 1; i < weight.size(); i++) { // 遍历物品
        for(int j = 0; j <= bagWeight; j++) { // 遍历背包容量
			// 如果背包容量j<当前物品重量weight[i]
            if (j < weight[i]) {
				dp[i][j] = dp[i - 1][j];
			}
            else {
				dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
			}

        }
    }

5、打印dp数组

最后打印dp数组：

//打印dp数组
	for (int i = 0; i < weight.size(); i++){
		for (int j = 0; j <5; j++){
			cout<<dp[i][j]<<" ";
		}
		cout <<endl;
	}

打印结果如下：

0 15 15 15 15 
0 15 15 20 35 
0 15 15 20 35 

二、代码实现

void bag_problem(int bagWeight,vector<int> & weight,vector<int>& value) {
    // 二维数组
    vector<vector<int>> dp(weight.size(), vector<int>(bagWeight + 1, 0));

    // 初始化
    for (int j = weight[0]; j <= bagWeight; j++) {
        dp[0][j] = value[0];
    }

    // weight数组的大小 就是物品个数
    for(int i = 1; i < weight.size(); i++) { // 遍历物品
        for(int j = 0; j <= bagWeight; j++) { // 遍历背包容量
			// 如果背包容量j<当前物品重量weight[i]
            if (j < weight[i]) {
				dp[i][j] = dp[i - 1][j];
			}
            else {
				dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
			}

        }
    }
	//打印dp数组
	for (int i = 0; i < weight.size(); i++){
		for (int j = 0; j <5; j++){
			cout<<dp[i][j]<<" ";
		}
		cout <<endl;
	}
}
int main()
{
   	cout << "Hello World"<<endl;
    int bagWeight = 4;// 背包重量
	vector<int> weight = {1, 3, 4}; //	物品重量
    vector<int> value = {15, 20, 30};// 物品价值
   	bag_problem(bagWeight,weight,value);
   	return 0;
}

使用滚动数组简化后：

void bag_problem(int bagWeight,vector<int> & weight,vector<int>& value) {
    // 一维数组及其初始化
    vector<int> dp(bagWeight + 1, 0);
    // 先遍历每个物品，再遍历不同的背包重量
    for(int i = 0; i < weight.size(); i++) { // 遍历物品
        for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量
			dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
        }
    }
	//打印dp数组
    for (int j = 0; j <bagWeight + 1; j++){
        cout<<dp[j]<<" ";
    }
    cout <<endl;
}
int main()
{
   	cout << "Hello World"<<endl;
    int bagWeight = 4;// 背包重量
	vector<int> weight = {1, 3, 4}; //	物品重量
    vector<int> value = {15, 20, 30};// 物品价值
   	bag_problem(bagWeight,weight,value);
   	return 0;
}